详解零知识证明算法Marlin

arkworks for marlin 

Marlin 

Fractal

RICS

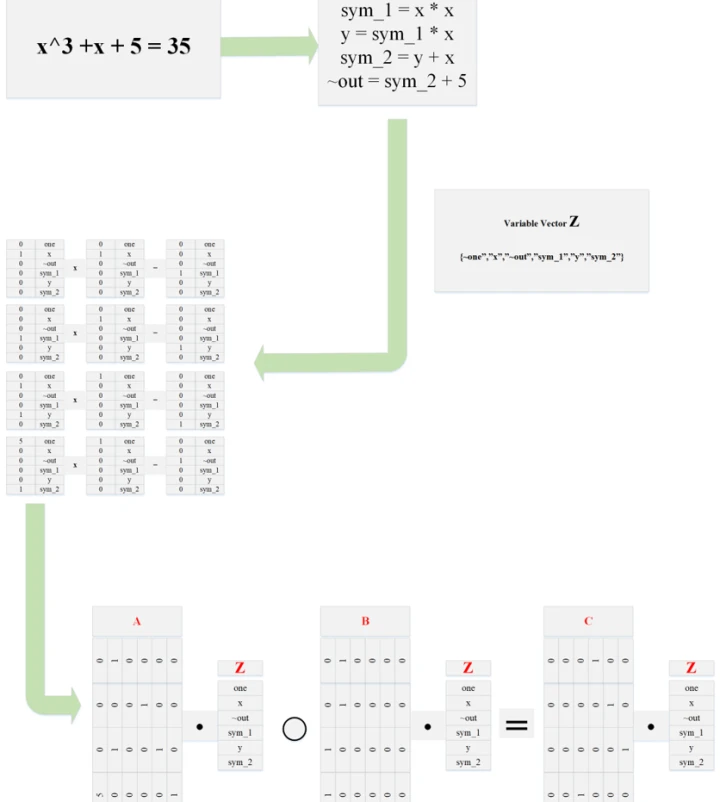
则R1CS成立。

Transition into Polynomial (efficiency）

Prepare

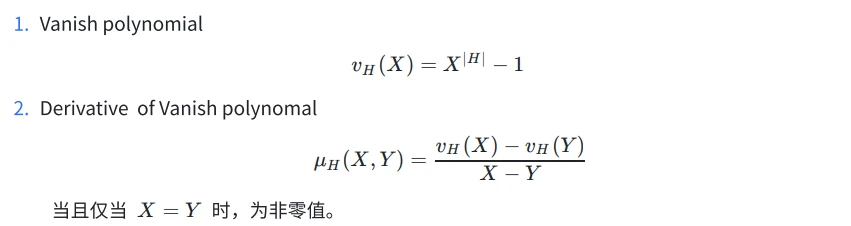
Define polynomial

2. 为向量 z = (x, w) 定义多项式（LDE）

3. 为矩阵 A, B, C 定义多项式（Holographic） 

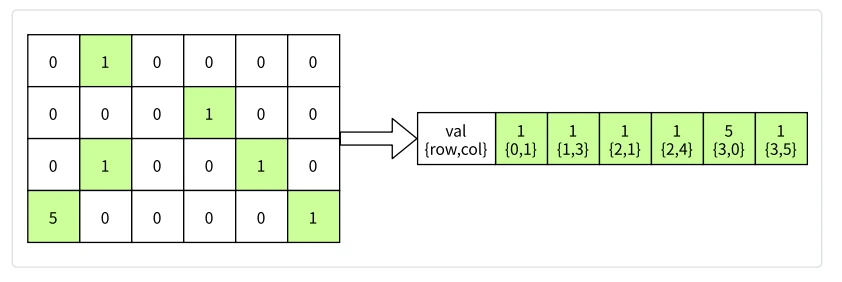
为了减小verifier计算的复杂度（见paper5.2.1），这⾥用了一个特殊的形式来表示矩阵，以上述示例的矩阵 A 为例：

Linearity check

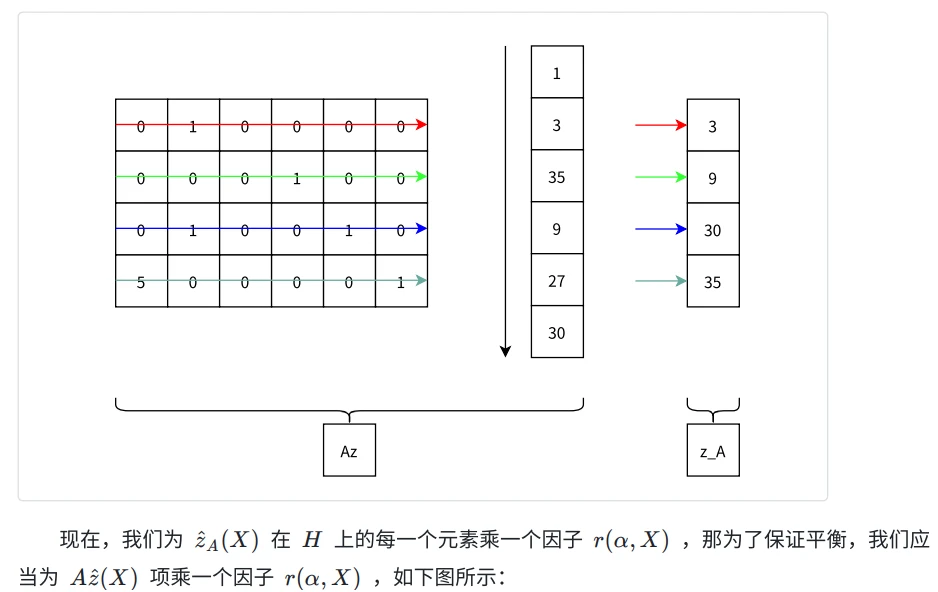
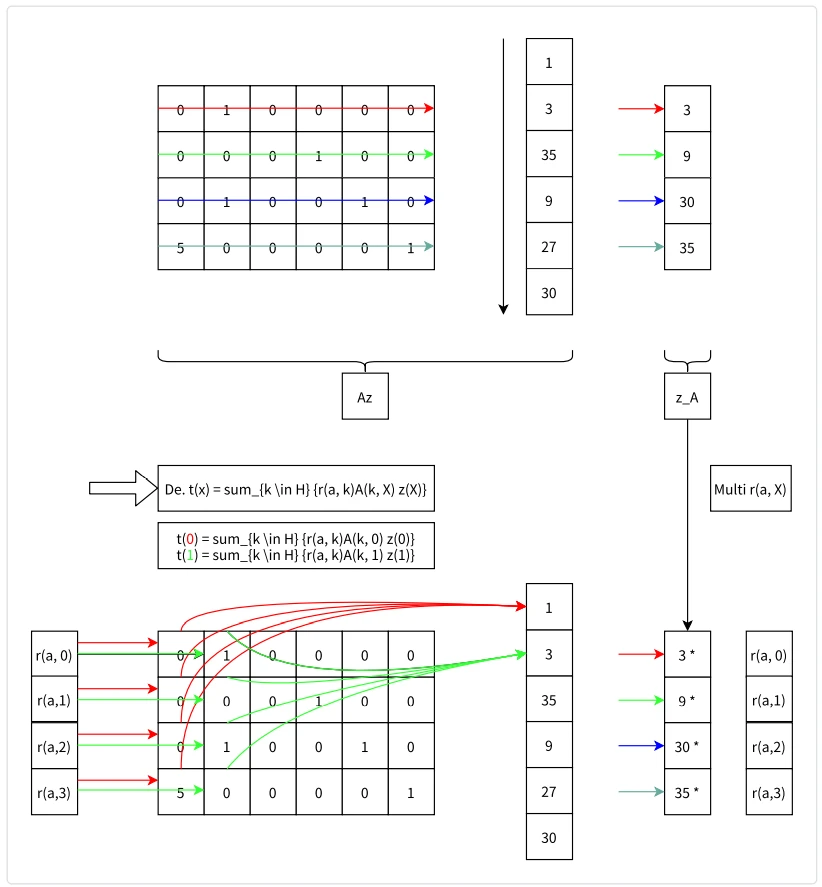
可以看出，当多项式 t(X) 取遍 H 值时，满足：

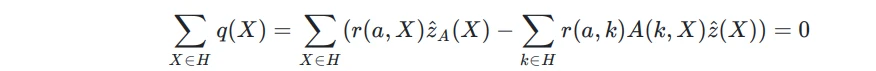
同样，也可以从公式推导：

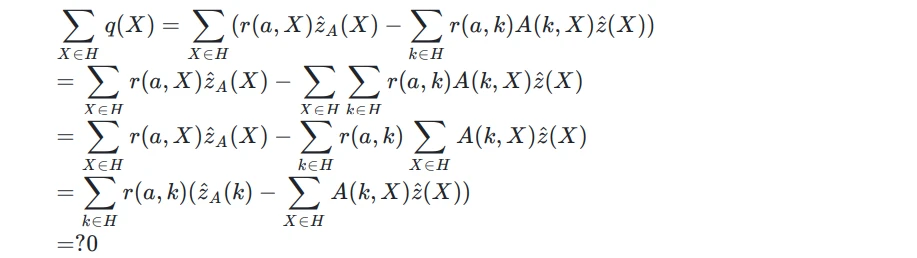
AHP for R1CS

Common

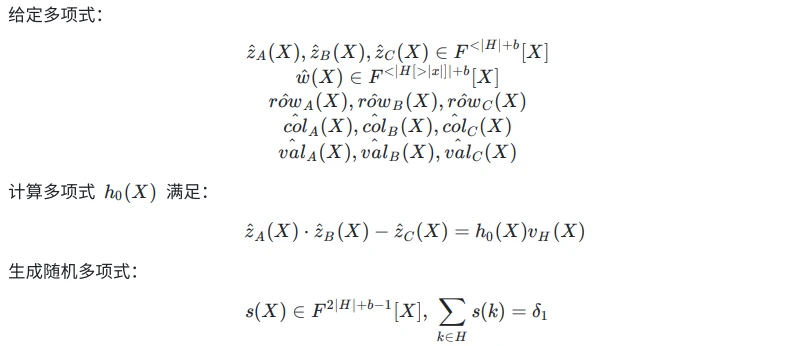
Prover

=>Prover

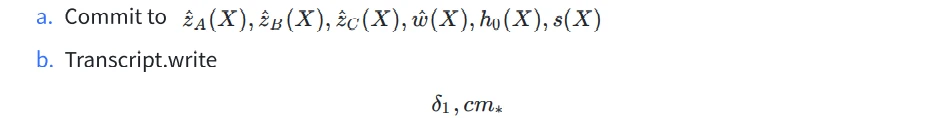
=>Oracle

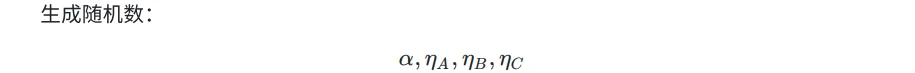
=>Prover - sumcheck-1

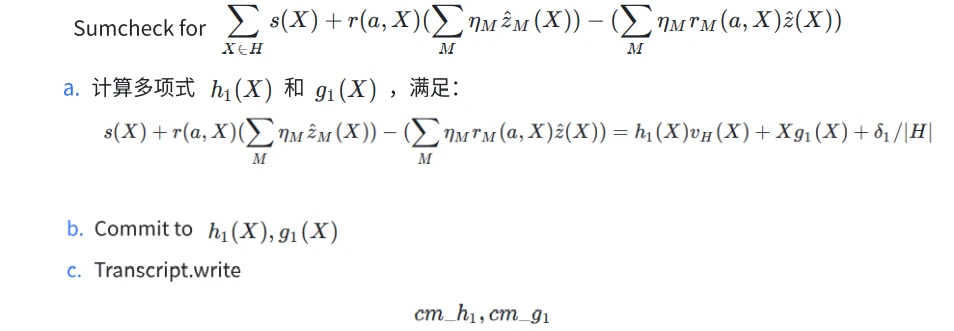
=> Oracle

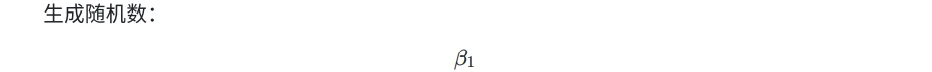=> Prover - sumcheck-1

=> Prover - sumcheck-2

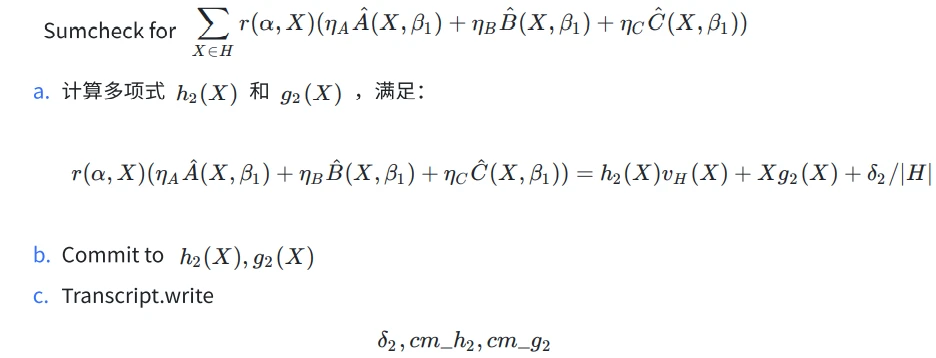
=> Oracle

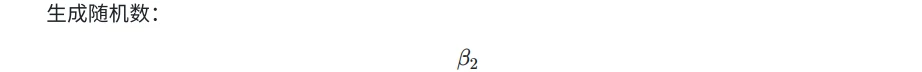
=> Prover - sumcheck-2

=> Prover - sumcheck-3

=> Oracle

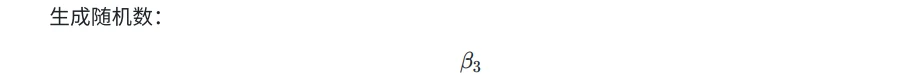
=> Prover - sumcheck-3

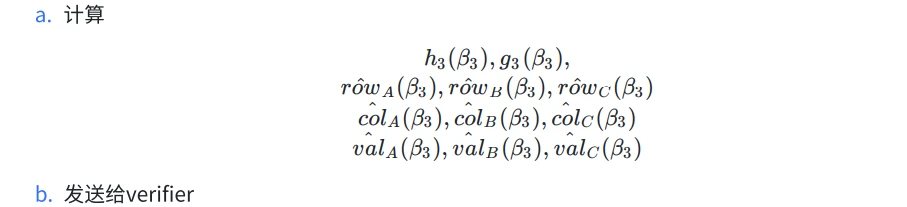
Verifier

=> Verifier-sumcheck-3

=> Verifier-sumcheck-2

Recall the equality

=> Verifier-sumcheck-1

Recall the equality

=> Verifier

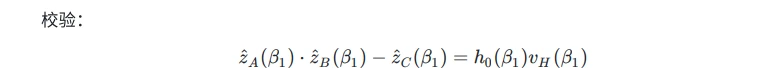
Polynomial commitment 

协议总共进行了三轮交互，每轮交互承诺的多项式，以及query的点如下：

Optimization

Sum(s(X)) = 0

生成随机多项式：

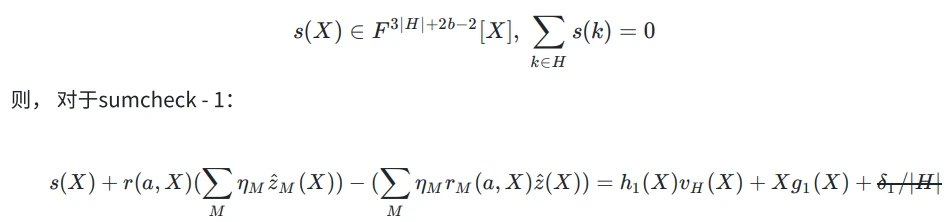
Reduce sumcheck 

根据COS20. Claim6.7（Fractal）论⽂提到的优化，我们令：

Common

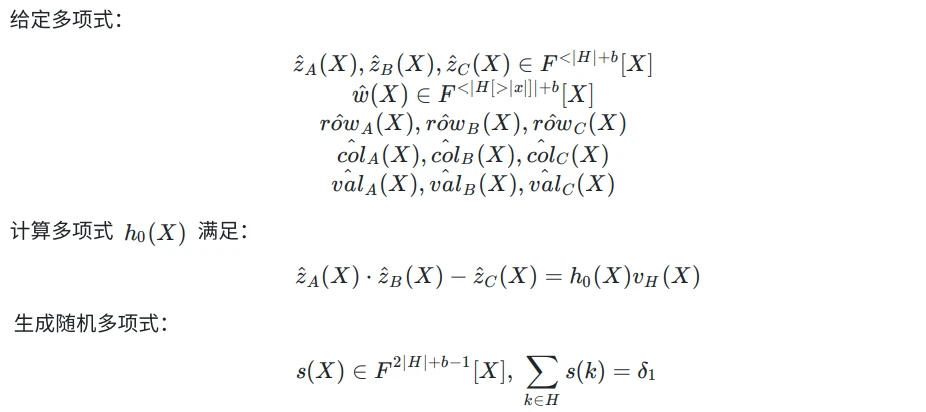
Prover

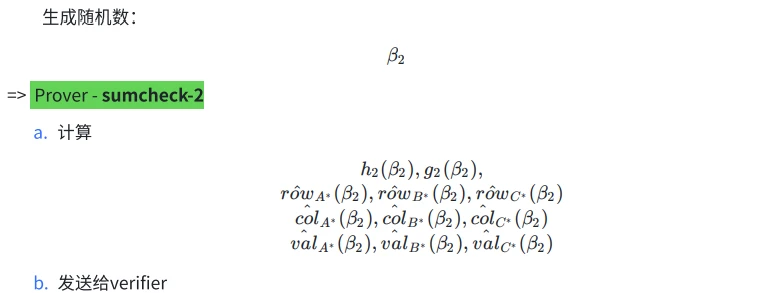
Verifier

Reduce polynomial numbers for Sumcheck - 2 

对三个矩阵的现行校验，压缩成对一个矩阵的校验，即：

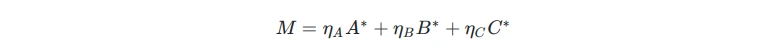
对这个多项式进行稀疏矩阵的表示。 

矩阵多项式，从9个缩减为3个。 

Set b = 1 

令 b = 1

Final Procotol 

Marlin in arkworks

关于我们

Sin7y成立于2021年，由顶尖的区块链开发者组成。我们既是项目孵化器也是区块链技术研究团队，探索EVM、Layer2、跨链、隐私计算、自主支付解决方案等最重要和最前沿的技术。

微信公众号：Sin7Y

GitHub | Twitter | Telegram | Medium| Mirror | HackMD | HackerNoon