
在区块链网络中,节点如何确保新提出的区块的所有数据都是可用的?这为什么重要?
在这篇文章中,我们将深入探讨数据可用性问题及其如何影响以太坊的扩展性。
数据可用性问题是什么?
数据可用性(DA)问题:区块链网络中的节点如何确保新提出的区块中的所有数据实际上是可用的?如果数据不可用,该区块可能包含由区块生产者隐藏的恶意交易。即使区块包含非恶意交易,隐藏它们也可能威胁到系统的安全。
例如,假设 Alice 是一个 ZK-Rollup 的运营者。她在以太坊上提交了一个 ZK-Proof 并得到验证。如果她没有在以太坊上提交所有交易数据,尽管她的证明证实了在 rollup 中进行的所有状态转换都是有效的,但 rollup 的用户仍可能对他们当前的账户余额一无所知。因为零知识的特性,提交的证明无法揭示当前状态的信息。
在 Optimistic Rollup 的场景中,也存在类似的例子,其中 Alice 在以太坊上提交了一个声明(assertion),但是由于交易数据不可用,OPR 的参与者无法重新计算或质疑该声明。
为了应对上述情况,OPR 和 ZKR 的设计都要求运营者将所有交易细节作为“calldata”提交到以太坊上。虽然这使它们在短期内避免了 DA 问题,但随着 rollup 内部交易数量的增加,需要提交的数据量也会增长,限制了这些 rollup 能够提供的扩展量。
更糟糕的是,数据不可用是一种无法唯一归因的错误。这意味着参与者无法向其他节点证明特定数据块缺失。这是因为 Bob 可以广播 Alice 提交的区块缺少数据,但当 Charlie 向 Alice 查询时,她可能会提供数据给他。
数据可用性问题怎么影响当前的区块链?
为回答这个问题,让我们首先回顾一下类似以太坊的区块链的一般区块结构,以及任何区块链网络上存在的客户端类型。
一个区块可以分为两个主要部分:
区块头:一个小的区块头包含与区块中包含的交易相关的摘要和元数据。
区块体:包含所有交易数据,构成区块的主要部分。
在传统的区块链协议中,所有节点都被视为完整节点,它们同步整个区块并验证所有状态转换。它们需要花费大量资源来检查交易的有效性并存储区块。优点是,这些节点不会接受任何无效的交易。
可能还有另一类节点,它们没有(或不想花费)资源来验证每笔交易。相反,它们主要对了解区块链的当前状态和一些对它们有关的交易是否被链包含感兴趣。理想情况下,这些轻客户端也应该被保护不受包含无效交易的链的欺骗。这实际上可以使用所谓的欺诈证明来实现。这些简洁的信息显示特定的区块体包含无效的交易。任何完整节点都可以产生这样的欺诈证明,因此轻客户端不必信任某个特定的完整节点是诚实的。它们只需确保它们与一个能够确保如果有区块头的欺诈证明可用,它们将接收到它的八卦网络连接良好。
然而,这个系统存在一个问题:如果一个区块生产者不透露一个区块背后的全部数据怎么办?在这种情况下,完整节点显然会拒绝这个区块,因为在它们看来,如果一个区块不附带区块体,那么它甚至不是一个区块。然而,轻客户端可以被展示区块头链,并且无法注意到数据缺失。同时,完整节点不能产生欺诈证明,因为它们缺少创建欺诈证明所需的数据。
为了应对这一问题,我们需要一种机制来让轻客户端验证数据可用性。这将确保隐藏数据的区块生产者不能通过说服轻客户端来逃避。这也会迫使区块生产者透露部分数据,使整个网络以协作的方式访问整个区块的数据。
让我们通过一个例子更深入地了解这个问题。假设区块生产者 Alice 构建了一个包含交易 tx 1、tx 2、...、txn 的区块 B。假设 tx 1 是一个恶意交易。如果 tx 1 被广播,任何完整节点都可以验证它是恶意的,并将这个信息作为欺诈证明发送给轻客户端,轻客户端会立即知道这个区块是不可接受的。然而,如果 Alice 想要隐藏 tx 1 ,她就只透露头部和除 tx 1 之外的所有交易数据。完整节点无法验证 tx 1 的正确性。
有人可能会认为一个简单的解决方案是让所有轻客户端随机抽样交易,如果他们发现他们的样本是可用的,他们就可以确信区块是可用的。但是让轻节点随机查询任意一笔交易,轻客户端查询 tx 1 的概率是 1/n。因此,Alice 几乎总能欺骗轻客户端接受一个恶意交易。换句话说,大多数轻客户端都会被欺骗。由于不可归因的性质,完整节点无法以任何方式证明 tx 1 是不可用的。不幸的是,增加样本数量也并不能使情况变得更好。
那么,我们该如何解决这个问题呢?
解决这个问题的方法在于在区块中引入冗余。在编码理论,特别是擦除编码方面,有一套丰富的文献可以帮助我们解决这个问题。
简而言之,擦除编码允许我们将任何 n 个数据块扩展成 2 n 个数据块,这样任何 2 n 中的 n 个就足以重构原始数据(参数是可调的,但这里我们为了简化而考虑这种情况)。
如果我们迫使区块生产者对交易 tx 1、tx 2、...、txn 进行擦除编码,那么要隐藏单个交易,它需要隐藏 n+ 1 个数据块,因为任何 n 个数据块都足以构建整个交易集。在这种情况下,少量的查询就能让轻客户端非常有信心地知道底层数据确实是可用的。
Woah, 所以就这样吗?
不。尽管这个简单的技巧使隐藏数据变得更加困难,但仍有可能区块生产者故意以错误的方式进行擦除编码。然而,完整节点可以验证这种擦除编码是否正确进行,如果没有,它可以向轻客户端证明这一点。这就是另一种类型的欺诈证明,就像上面提到的恶意交易一样。有趣的是,只需一个诚实的完整节点作为轻客户端的邻居,就能确保如果区块是恶意的,那么它将收到一个欺诈证明。这确保了轻客户端能够以非常高的概率访问一个没有恶意交易的链。
但有一个问题。如果做得过于简单,一些欺诈证明的大小可能会和区块本身的大小一样大。我们对轻客户端的资源假设禁止我们使用这样的设计。通过使用多维擦除编码技术,已经有了改进,这些技术降低了欺诈证明的大小,但代价是增加了承诺的大小。为了简洁起见,我们不在这里详细介绍这些,但这篇论文对此进行了详细的分析。
基于欺诈证明的解决方案的问题在于,轻客户端永远无法完全确定任何它尚未收到欺诈证明的区块。同时,它们继续信任其完整节点是诚实的。诚实的节点也需要得到激励,以持续审核区块。
我们在这里关注的是那些系统,它们保证如果区块编码无效,完整节点可以检测到并向轻客户端提供证明,以说服它们存在不当行为。然而,在下一部分中,我们将关注那些保证只有有效编码能被提交到链上的区块编码。这消除了需要证明编码错误的欺诈证明的需求。基于有效性证明的解决方案使应用程序能够在不必等待完整节点提供这类欺诈证明的情况下使用系统。
那么,这些解决方案是如何工作的?
近期,多项式承诺在区块链领域引起了重新的兴趣。这些多项式承诺,特别是对多项式的恒定大小的 KZG/Kate 承诺,可以用来设计一个不需要欺诈证明的整洁的数据可用性(DA)方案。简而言之,KZG 承诺允许我们使用单个椭圆曲线群元素来承诺一个多项式。此外,该方案支持我们证明在某个点 i 上,多项式 φ 的值为 φ(i),使用恒定大小的见证。这种承诺方案在计算上是约束性的,并且也是同态的,允许我们巧妙地避开欺诈证明。
我们强制区块生产者将原始交易数据排列成一个大小为 n x m 的二维矩阵。它使用多项式插值将每列的大小 n 扩展为大小 2 n 的列。这个扩展矩阵的每一行生成一个多项式承诺,并将这些承诺作为区块头的一部分发送。下面给出了区块的示意性表示。
轻客户端查询这个扩展矩阵的任何一个单元格以获取证明,这使得它能够立即根据区块头进行验证。恒定大小的成员身份证明使得采样极为高效。承诺的同态特性确保只有在区块构建正确时,证明才能被验证,而多项式插值确保了恒定数量的成功样本意味着数据可用性的可能性非常高。
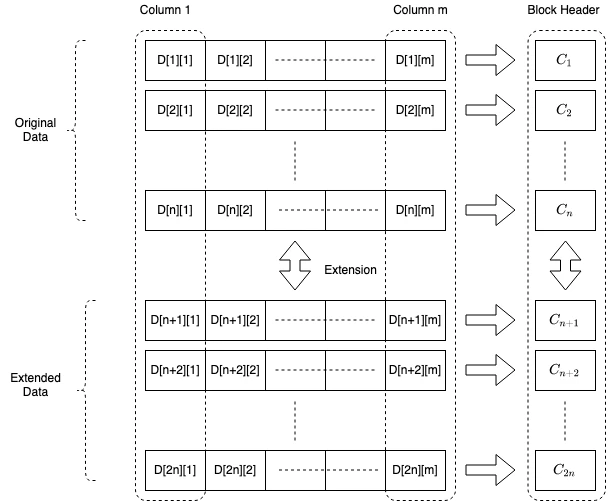
区块的示意性表示
这个方案的更细节部分,以及进一步的优化和成本估算,超出了本文的范围。然而,我们想指出的是,虽然我们在这里讨论的是一个二维方案,但类似的保证也可以通过一个一维方案提供,一维方案的区块头大小更小,但代价是减少了并行性和轻客户端采样效率。我们将在后续文章中更深入地探讨这一点。
其他替代方案是什么?接下来会发生什么?
高维擦除编码和 KZG 承诺并不是解决数据可用性问题的唯一方法。我们在这里略过了其他一些方法,如编码默克尔树、编码交错树、FRI 和基于 STARK 的方法,但每种方法都有其优点和缺点。
在 Avail,我们一直在使用 KZG 承诺开发数据可用性解决方案。在后续的文章中,我们将介绍实现细节,如何使用它,以及我们如何计划改变数据可用性问题空间。欲了解更多关于 Avail 的信息,请在 Twitter上关注我们,并加入我们的 Discord 服务器。
Twitter:https://twitter.com/AvailProject
Discord:https://discord.com/invite/jTkvDrZ54r
也欢迎关注 Modular 101 的 Twitter 账号:@Modular 101










