实用性拜占庭容错算法(Practical Byzantine Fault Tolerance,PBFT),是一种在信道可靠的情况下解决拜占庭将军问题的实用方法。拜占庭将军问题最早由Leslie Lamport等人在1982年发表的论文[1]提出,论文中证明了在将军总数n大于3f,背叛者为f或者更少时,忠诚的将军可以达成命令上的一致,即3f+1<=n,算法复杂度为O(n^(f+1))。随后Miguel Castro和Barbara Liskov在1999年发表的论文[2]中首次提出PBFT算法,该算法容错数量也满足3f+1<=n,算法复杂度降低到了O(n^2)。
如果对于PBFT共识算法有所了解,对节点总数n与容错上限f的关系可能会比较熟悉:在系统内最多存在f个错误节点的前提下,系统内总节点数量n应该满足n>3f,在推进共识过程中则需要收集一定数目的投票,才能完成认证过程。在本节当中,我们将首先讨论这些数值间关系该如何得出。
--Quorum机制--
在有冗余数据的分布式存储系统当中,冗余数据对象会在不同的机器之间存放多份拷贝。但是在同一时刻,一个数据对象的多份拷贝只能用于读或者写。为了保持数据冗余与一致性,需要对应的投票机制进行维持,这就是Quorum机制。区块链作为一种分布式系统,同样也需要该机制进行集群维护。
为了更好地理解Quorum机制,我们先来了解一种与之类似,但是更加极端的投票机制——WARO机制(Write All Read One)。使用WARO机制维护节点总数为n的集群时,节点执行写操作的“票数”应当为n,而读操作时的“票数”可以设置为1。也就是说,在执行写入时,需要保证全部节点完成写入操作才可视该操作为完成,否则会写入失败;相应地,在执行读操作时,只需要读取一个节点的状态,就可以对该系统状态进行确认。可以看到,在使用WARO机制的集群中,写操作的执行非常脆弱:只要有一个节点执行写入失败,那么这次操作就无法完成。不过,虽然牺牲了写操作健壮性,但是,在WARO机制下,对于该集群执行读操作会非常容易。
Quorum机制[3]就是对读写操作的折衷考虑,对于同一份数据对象的每一份拷贝,不会被超过两个访问对象读写,并且权衡读写时的集合大小要求。在一个分布式集群当中,每一份数据拷贝对象都被赋予了一票。假设:
系统中有V票,这就意味着一个数据对象有V份冗余拷贝;
对于每一个读操作,获得的票数必须不小于最小读票数R(read quorum)才可以成功读取;
对于每个写操作,获得的票数必须不小于最小写票数W(write quorum)才可以成功写入。
此时,为了维持集群一致性,V、R、W应满足不等关系,R+W>V且W>V/2。其中,R+W>V保证了一个数据不会被同时读或写。当一个写操作请求传入,它必须要获得W票,而剩下的数量是V-W不足R,因此不会再处理读请求。同理,当读请求已经获得了R票,写请求就无法被处理。W>V/2,保证了数据的串行修改,也就是说,一份数据的冗余拷贝不可能同时被两个写请求修改。
对于集群中的共识节点,在推进共识算法时,参与共识的节点会同时对集群进行读写操作。为了平衡读写操作对于集合大小的要求,每个节点的R与W取同样大小,记为Q。当集群中总共存在n个节点,并且其中最多出现f个错误节点的情况下,我们该如何计算n、f、Q之间的关系呢?接下来,我们将从最简单的CFT场景出发,逐步探索如何在BFT场景中得到这些数值取值之间的关系。
▲CFT
CFT(Crash Fault Tolerance),表示系统中的节点只会出现宕机(Crash)这种错误行为,任何节点不会主动发出错误消息。当我们在讨论共识算法可靠性时,通常会关注算法两种基本性质:活性(liveness)与安全性(safety)。在计算Q的大小时,同样也可以从这两个角度出发进行考虑。
对于活性与安全性,有一种比较直观的描述方式:
something eventually happens[4],某个事件最终会发生
something good eventually happens[4],这个最终会发生的事件合理
从活性角度出发,我们的集群需要能够持续运行下去,不会由于某些节点的错误导致无法继续共识。从安全性角度出发,我们的集群在共识推进的过程中,能够持续获得某个合理的结果,对于分布式系统来说,这种“合理”的结果,其最基本的要求就是集群整体状态的一致性。
于是,在CFT场景下,对于Q数值的确定就变得简单明确:
活性:由于我们需要保证集群能够持续运行,所以,在任何场景下都要保证有获取到Q票的可能性,从而为集合读写数据。由于集群中最多会有f个节点发生宕机,所以为了保证能获取到Q票,该值的大小需要满足:Q<=n-f。
安全性:由于我们需要保证集群不发生分歧,所以,按照Quorum机制的基本要求,需要满足在上一节当中提到的两个不等式,将Q作为最小读集合与最小写集合带入该组不等式,此时,Q满足不等关系,Q+Q>n且Q>n/2,因此,该值的大小需要满足:Q>n/2。
▲BFT
BFT(Byzantine Fault Tolerance),表示集群中的错误节点不仅可能会发生宕机,也可能存在恶意行为,即拜占庭(Byzantine)行为,例如主动进行状态分叉。在这种情况下,对于集群整体而言,只有n-f个节点的状态可靠,当我们收集到Q个投票时,其中也只有Q-f个投票来自可靠的节点。因此,在安全性方面,BFT场景下需要保证状态可靠的节点之间不会发生分歧,因此得到以下两种关系:
活性:依然只需要保证每时每刻都有获取Q票的可能性,因此,Q<=n-f。
安全性:对于全部保证正确的节点(总数n-f)不会发生分歧,此时,应当满足不等关系,(Q-f)+(Q-f)>n-f且(Q-f)>(n-f)/2,因此,此时Q的大小需要满足的关系为,Q>(n+f)/2。
▲节点总数与容错上限
对于节点总数n与容错上限f,在PBFT论文当中给出的解释[1]:由于存在f个节点可能发生宕机,因此我们至少需要在收到n-f条消息时进行响应,而对于我们收到的来自n-f个节点的消息,由于其中最多可能存在f条消息来自于不可靠的拜占庭节点,因此需要满足n-f-f>f,所以,n>3f。
简单来说,PBFT的作者从集群活性与安全性出发,得到了节点总数与容错上限之间的关系。上一节中,我们也是从活性与安全性角度,获得了n、f与Q的关系,在这里也可以用来推导n与f的关系:为了同时满足活性与安全性的要求,Q需要满足不等关系,Q<=n-f且Q>(n+f)/2,因此,可以得到n与f之间的不等关系,(n+f)/2<n-f,也就是n>3f。
(通过类似的方式,也可以得到CFT场景中n与f的关系,n>2f。)
--PBFT与RBFT --
在理解BFT场景中n、f、Q的关系后,接下来进入到PBFT的介绍。在此之前,简单提一下SMR(State Machine Replication)复制状态机[5]。在该模型当中,对于不同的状态机,如果从同样的初始状态出发,按照同样的顺序输入同样的指令集,那么它们得到的最终结果总会一致。对于共识算法而言,其只需要保证“按照同样的顺序输入同样的指令”,即可在各个状态机上获得同样的状态。而PBFT就是对指令执行顺序的共识。
那么,PBFT是如何保证指令执行顺序的一致性呢?PBFT集群为主从结构,由主节点提出提案,并通过集群中各个节点间的交互进行验证,从而使得每个正确节点遵循同样的顺序对指令集进行执行。在这个交互过程中,就需要使用Quorum机制保证集群整体状态的一致性。下面我们将对PBFT进行详细介绍。
▲两阶段共识
相比较常见的“三阶段“概念(pre-preapre、prepare、commit),将PBFT视为一种两阶段共识协议或许更能体现每个阶段的目的:提案阶段(pre-prepare与prepare)和提交阶段(commit)。在每个阶段中,各个节点都需要收集来自Q个节点一致的投票后,才会进入到下一个阶段。为了更方便讨论,这里将讨论节点总数为3f+1时的场景,此时,读写集票数Q为2f+1。
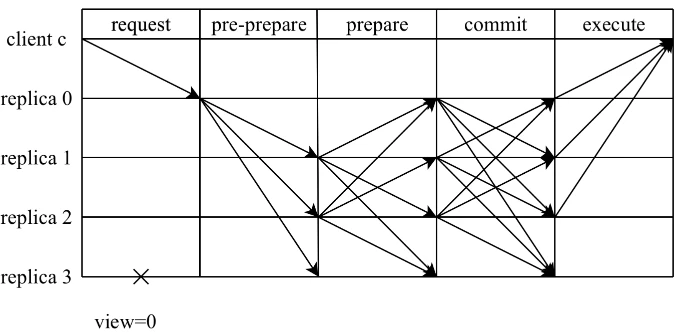
1) 提案阶段
在该阶段中,由主节点发送pre-prepare发起共识,由从节点发送prepare对主节点的提案进行确认。主节点在收到客户端的请求后,会主动向其它节点广播pre-prepare消息<pre-prepare, v, n, D(m)>
v为当前视图
n为主节点分配的请求序号
D(m)为消息摘要
m为消息本身
从节点在收到pre-prepare消息之后,会对该消息进行合法性验证,若通过验证,那么该节点就会进入pre-prepared状态,表示该请求在从节点处通过合法性验证。否则,从节点会拒绝该请求,并触发视图切换流程。当从节点进入到pre-prepared状态后,会向其它节点广播prepare消息<prepare, v, n, D(m), i>,
i为当前节点标识序号
其他节点收到消息后,如果该请求已经在当前节点进入pre-prepared状态,并且收到2f条来自不同节点对应的prepare消息(包含自身),从而进入到prepared状态,提案阶段完成。此时,有2f+1个节点认可将序号n分配给消息m,这就意味着,该共识集群已经将序号n分配给消息m。
2) 提交阶段
当请求在当前节点进入prepared状态后,本节点会向其它节点广播commit消息<commit, v, n, i>。如果该请求已经在当前节点达到prepared状态,并且收到2f+1条来自不同节点对应的commit消息(包含自身),那么该请求就会进入到committed状态,并可以进行执行。此时,有2f+1个节点已经得知共识集群已经将序号n分配给消息m。执行完毕后,节点会将执行结果反馈给客户端进行后续判断。
▲检查点机制
PBFT共识算法在运行过程中,会产生大量的共识数据,因此需要执行合理的垃圾回收机制,及时清理多余的共识数据。为了达成这个目的,PBFT算法设计了checkpoint流程,用于进行垃圾回收。
checkpoint即检查点,这是检查集群是否进入稳定状态的流程。在进行检查时,节点广播checkpoint消息<checkpoint, n, d, i>
n为当前请求序号
d为消息执行后获得的摘要
i为当前节点表示
当节点收到来自不同节点的2f+1条有相同<n,d>的checkpoint消息后,即可认为,当前集群对于序号n进入了稳定检查点(stable checkpoint)。此时,将不再需要stable checkpoint之前的共识数据,可以对其进行清理。不过,如果为了进行垃圾回收而频繁执行checkpoint,那么将会对系统运行带来明显负担。所以,PBFT为checkpoint流程设计了执行间隔,设定每执行k个请求后,节点就主动发起一次checkpoint,来获取最新的stable checkpoint。
除此之外,PBFT引入了高低水位(high/low watermarks)的概念,用于辅助进行垃圾回收。在共识进行的过程中,由于节点之间的性能差距,可能会出现节点间运行速率差异过大的情况。部分节点执行的序号可能会领先于其他节点,导致于领先节点的共识数据长时间得不到清理,造成内存占用过大的问题,而高低水位的作用就是对集群整体的运行速率进行限制,从而限制了节点的共识数据大小。
高低水位系统中,低水位记为h,通常指的是最近一次的stable checkpoint对应的高度。高水位记为H,计算方式为H=h+L,L代表了共识缓存数据的最大限度,通常为checkpoint间隔K的整数倍。当节点产生的checkpoint达到到stable checkpoint状态时,节点将更新低水位h。在执行到最高水位H时,如果低水位h没有被更新,节点会暂停执行序号更大的请求,等待其他节点的执行,待低水位h更新后重新开始执行更大序号的请求。
▲视图变更
当主节点超时无响应或者从节点集体认为主节点是问题节点时,就会触发视图变更(view-change)。视图变更完成后,视图编号将会加1,随之主节点也会切换到下一个节点。如图所示,节点0发生异常触发视图变更流程,变更完成后,节点1成为新的主节点。
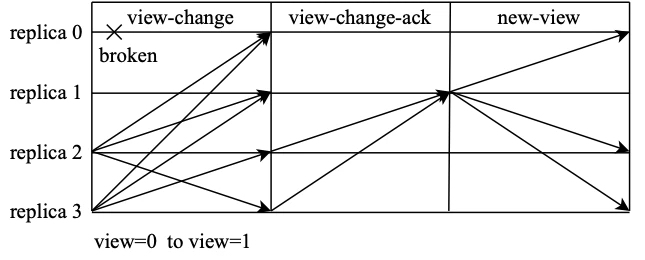
当视图变更发生时,节点会主动进入到新视图v+1中,并广播view-change消息,请求进行主节点切换。此时,共识集群需要保证,在旧视图中已经完成共识的请求能够在新视图中得到保留。因此,在视图变更请求中,一般需要附加部分旧视图中的共识日志,节点广播的请求为<viewchange, v+1, h, C, P, Q, i>
i为发送者节点的身份标识
v+1表示请求进入的新视图
h为当前节点最近一次的稳定检查点的高度
C:当前节点已经执行过的检查点的集合,数据按照<n,d>的方式进行存储,表示当前节点已经执行过序号为n摘要为d的checkpoint检查,并发送过相应的共识消息。
P:在当前节点已经达成prepared状态的请求的集合,即,当前节点已经针对该请求收到了1条pre-prepare消息与2f条prepare消息。在集合P中,数据按照<n,d,v>的方式进行存储,表示在视图v中,摘要为d序号为n的请求已经进入了prepared状态。由于请求已经达成了prepared状态,说明至少有2f+1个节点拥有并且认可该请求,只差commit阶段即可完成一致性确认,因此,在新的视图中,这一部分消息可以直接使用原本的序号,无需分配新序号。
Q:在当前节点已经达成pre-prepared状态的请求的集合,即,当前节点已经针对该请求发送过对应的pre-prepare或prepare消息。在集合Q中,数据同样按照<n,d,v>的方式进行存储。由于请求已经进入pre-prepared状态,表示该请求已经被当前节点认可。
但是,视图v+1对应的新主节点P在收到其他节点发送的view-change消息后,无法确认view-change消息是否拜占庭节点发出的,也就无法保证一定使用正确的消息进行决策。PBFT通过view-change-ack消息让所有节点对所有它收到的view-change消息进行检查和确认,然后将确认的结果发送给P。主节点P统计view-change-ack消息,可以辨别哪些view-change是正确的,哪些是拜占庭节点发出的。
节点在对view-change消息进行确认时,会对其中的P、Q集合进行检查,要求集合中的请求消息小于等于视图v,若满足要求,就会发送view-change-ack消息<viewchange-ack, v+1, i, j, d>
i为发送ack消息的节点标识
j为要确认的view-change消息的发送者标识
d为要确认的view-change消息的摘要
不同于一般消息的广播,这里不再使用数字签名标识消息的发送方,而是采用会话密钥保证当前节点与主节点通信的可信,从而帮助主节点判定view-change消息的可信性。
新的主节点P维护了一个集合S,用来存放验证正确的view-change消息。当P获取到一条view-change消息以及合计2f-1条对应的view-change-ack消息时,就会将这条view-change消息加入到集合S。当集合S的大小达到2f+1时,证明有足够多的非拜占庭节点发起视图变更。主节点P会按照收到的view-change消息,产生new-view消息并广播,<new-view, v+1, V, X>
V:视图变更验证集合,按照<i,d>的方式进行存储,表示节点i发送的view-change消息摘要为d,均与集合S中的消息相对应,其他节点可以使用该集合中的摘要以及节点标识,确认本次视图变更的合法性。
X:包含稳定检查点以及选入新视图的请求。新的主节点P会按照集合中S的view-change消息进行计算,根据其中的C、P、Q集合,确定最大稳定检查点以及需要保留到新视图中的请求,并将其写入集合X中,具体选定过程相对繁琐,如果有兴趣,读者可以参阅原始论文[6]。
▲改进空间与RBFT
RBFT(Robust Byzantine Fault Tolerance),是趣链科技基于PBFT为企业级联盟链平台研发的高鲁棒性共识算法。相比较PBFT来说,我们在共识消息处理、节点状态恢复、集群动态维护等多方面进行了优化改良,使得RBFT共识算法能够应对更复杂多样的实际场景。
1) 交易池
包括RBFT在内,许多共识算法的工业实现中,都设计了独立的交易池模块。在收到交易后,将交易本身存放在交易池里,并通过交易池对交易进行共享,使得各个共识节点都能获得共享的交易。在共识的过程中,只需对交易哈希进行共识即可。
在处理较大交易时,交易池对于共识的稳定性有不错的提升。将交易池与共识算法本身进行解耦,也更方便通过交易池实现更多的功能特性,比如交易去重。
2) 主动恢复
在PBFT中,当节点借由checkpoint或view-change发现自身的低水位落后,即稳定检查点落后时,落后节点就会触发相应的恢复过程,以拉取该稳定检查点之前的数据。这样的落后恢复机制有一些不足:一方面,该恢复流程的触发是被动的,需要在checkpoint过程或者触发view-change完成时才能触发落后恢复;另一方面,对于落后节点来说,如果通过checkpoint发现自身稳定检查点落后时,落后节点只能恢复到最新的稳定检查点,而无法获得该检查点后落后的共识消息,可能一直无法真正参与到共识当中。
在RBFT中,我们设计了主动的节点恢复机制:一方面,该恢复机制可以主动触发,更快地帮助落后节点进行恢复;另一方面,在恢复到最新的稳定检查点基础之上,我们设计了水位间的恢复机制,从而使得落后节点能够获取到最新的共识消息,更快地参与到正常共识流程。
3) 集群动态维护
Raft作为一种广泛应用在工程中的共识算法,其重要优势之一,就是能够动态完成集群成员变更。而PBFT没有给出集群成员动态变更方案,在实际应用中存在不足。在RBFT中,我们设计了一种动态变更集群成员的方案,使得不需要停启集群整体的情况下,就可以对集群成员进行增删。
新增或删除节点时,由管理员向集群发交易创建操作节点的提案,并等待其他管理员投票,投票通过后由创建提案的管理员再次向集群发执行提案配置交易,执行时会更改集群配置。
对于共识部分,当处理执行提案配置交易时,集群中的节点将进入配置变更状态,不再打包其他交易。主节点将该交易单独打包生成配置包,并对该配置包进行共识。当该配置包完成共识,它将被执行并生成配置区块。为了保证改配置区块不可回滚,共识层将等待改配置包的执行结果,确定集群中已经对于该配置包所在高度形成稳定检查点,才会解除节点的配置状态,继续进行其他交易的打包。
对于集群不同的配置状态,我们通过世代(epoch)进行区分。不同世代拥有其独立的编号,该编号为单调递增的,每次执行完成一笔执行提案配置交易,将会对世代编号进行更新。对于集群中不同的节点,如果它们处于同一个世代下,则可以进行正常的信息交互。否则,节点之间只能进行状态恢复相关消息的交互。由于配置变更的信息已经被写入链上,因此,我们可以通过直接同步区块的方式为落后节点进行配置更新。通过上一节所说的主动恢复协议,世代落后的节点可以获取到最新的状态,并通过直接同步区块的方式恢复至最新的稳定检查点,同时完成节点世代与配置状态的恢复。
通过这样的动态变更集群成员的方式,使得集群配置维护更加可靠与便捷,并且可以为动态修改更多配置信息提供了可能。
作者简介
王广任
趣链科技基础平台部共识算法研究小组
参考文献
[1] Lamport L, Shostak R, Pease M. The Byzantine generals problem[M]//Concurrency: the Works of Leslie Lamport. 2019: 203-226.
[2] Castro M, Liskov B. Practical Byzantine fault tolerance[C]//OSDI.1999, 99(1999): 173-186.
[3] https://en.wikipedia.org/wiki/Quorum _ (distributed_computing)
[4] Owicki S, Lamport L. Proving liveness properties of concurrent programs[J]. ACM Transactions on Programming Languages and Systems (TOPLAS), 1982, 4(3): 455-495.
[5] Fred B. Schneider. Implementing fault-tolerant services using the state machine approach: A tutorial. ACM Comput. Surv., 22(4):299–319, 1990.
[6] Castro M, Liskov B. Practical Byzantine fault tolerance andproactive recovery[J]. ACM Transactions on Computer Systems (TOCS), 2002,20(4): 398-461.










