Original author: Weikeng Chen

In the Ethereum Virtual Machine (EVM), the Keccak hash function is widely used in the construction and verification of state trees (Merkle Patricia Trees), accounting for the main computational overhead in zero-knowledge proofs. How to efficiently prove Keccak is a long-standing technical problem in the field of zero-knowledge proofs.
To address this challenge, the Polyhedra team introduced Binary GKR, a high-performance proof system designed for Keccak and other binary operations.
Core progress: Keccak proof speed increased by 5.7 times
Binary GKR achieves the fastest Keccak zero-knowledge proof performance to date, which is about 5.7 times faster than the optimal solution of the existing binary proof system FRI-Binius. This breakthrough is not only of great theoretical significance, but also opens up new possibilities for practical applications.
Application prospects: zkEVM’s “universal acceleration sidecar”
We believe that Binary GKR can serve as a “universal acceleration sidecar” in a variety of zkEVM architectures, efficiently processing a large number of Keccak operations in the Ethereum state tree, thereby significantly reducing proof costs and improving system throughput and response speed.
Polyhedra will continue to promote the productization and open source process of Binary GKR, enabling the upgrade of zk architecture in Ethereum and the broader ecosystem.
Keccak: The Holy Grail of Zero-Knowledge Ethereum
Ethereum is gradually evolving towards a zero-knowledge proof native Layer-1. The Ethproofs project, which involves 21 teams and covers 22 ZK(E)VM implementations, is attempting to fully prove Ethereums historical blocks, taking a key step forward.
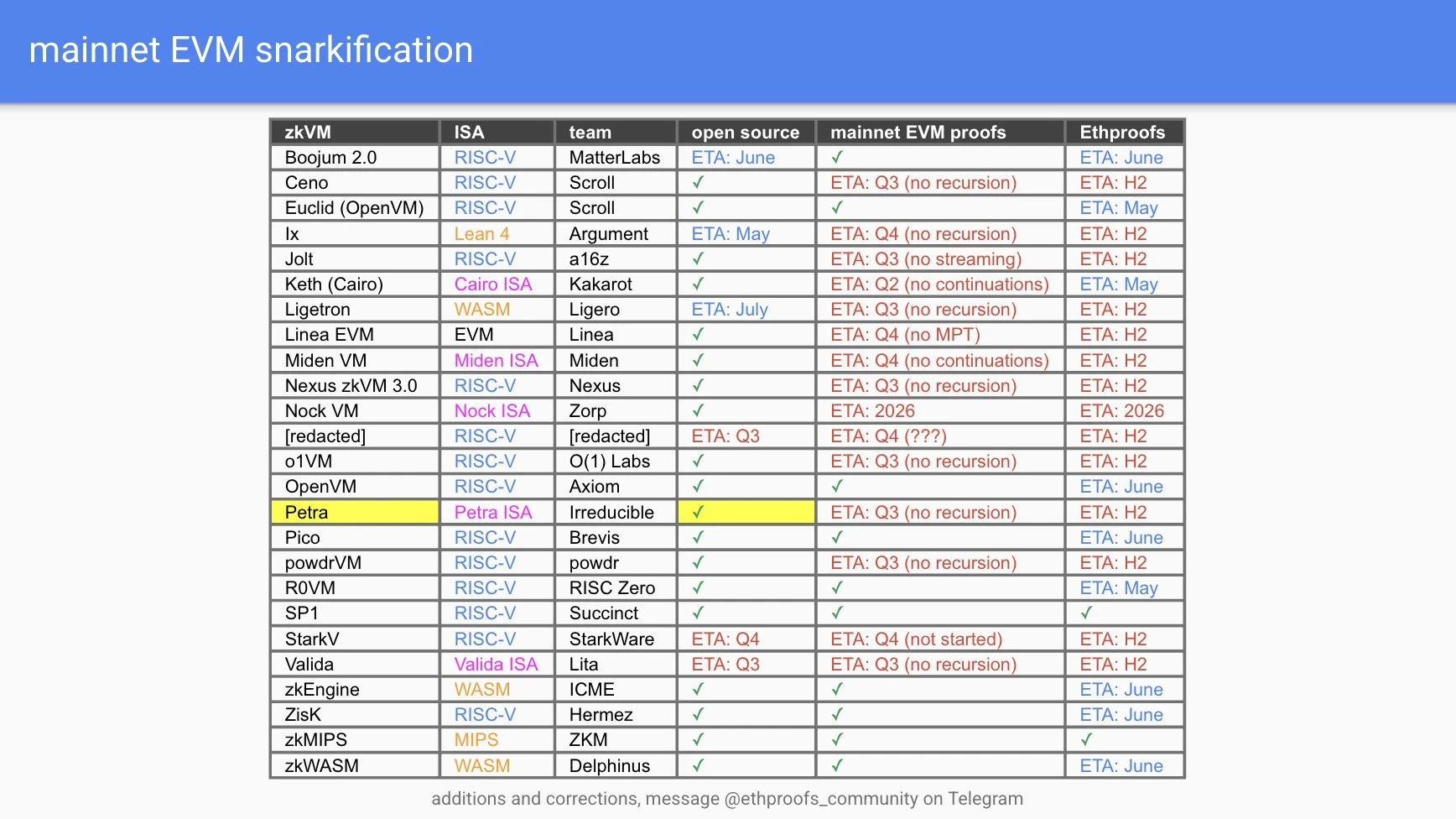
On the Ethproofs official website, you can view the progress of multiple teams in real time: projects such as ZkCloud, Succinct, Snarkify and ZKM have begun to continuously submit ZK proofs for the latest blocks. The ultimate goal of this trend is to build Ethereum into an execution layer driven by zero-knowledge proofs, while the consensus layer only needs to complete lightweight tasks such as proposing transaction lists.
The biggest challenge facing the zkEVM architecture: Keccak’s proof efficiency bottleneck
Currently, there are several Ethereum-compatible zkRollup projects (such as Polygon, Taiko, and Scroll) that have attempted to implement zkEVM. However, some operations in the traditional EVM that are efficient on the CPU are costly in the zero-knowledge proof system. The main performance bottleneck is the Keccak hash function.
Keccak is widely used to build Ethereums Merkle Patricia Tree, which records the entire chain status in hash form. However, Keccaks underlying operations are based on bit-level operations, which are incompatible with the prime field operation model used by most ZK systems, resulting in a significant performance degradation.
To help understand why the Keccak hash function is essentially a collection of bit operations, we briefly show five of its core operations: θ (theta), ρ (rho), π (pi), χ (chi), and ι (iota). These operations are applied to a 5 × 5 matrix structure, where each cell is a 64-bit integer, which we call a word. The entire matrix contains 5 rows and 5 columns.
θ (Theta): First, the parity value of each column is calculated, and then the parity value is exclusive-ored with the adjacent column on the left; at the same time, the adjacent column on the right is rotated left and then exclusive-ored. This process involves basic binary operations such as exclusive-or and left rotation.
ρ (Rho): Rotate each word in the matrix left bit by bit. The rotation distance of each word is different, but all are preset fixed values. This step is completely composed of left rotation operations.
π (Pi): Rearrange the words in the matrix according to a fixed pattern. Since this process is only a position permutation, it is often regarded as a zero-cost operation in zero-knowledge proofs.
χ (Chi): Perform bitwise combination operations along each row, and each word is combined with the two words adjacent to it on the left and right in the row. The operations include exclusive or, negation and and.
ι (Iota): Perform an XOR operation on the first word in the matrix with a fixed constant, which only involves the XOR operation.
The main challenge in implementing Keccak in zero-knowledge proofs is how to efficiently represent these bit-level operations, especially when each operation acts on a 64-bit integer. This is why we call it Keccak-1600 - because the state space of each round is 5 × 5 × 64 = 1600 bits. This operation process needs to be repeated 24 times.
Next, we briefly review some previous attempts to implement Keccak.
Attempt 1: Proof system based on Groth 16 or other R 1 CS
The most popular and direct way is to use Groth 16 or other R 1 CS (Rank-1 Constraint System) proof systems to implement Keccak. In order to express bit operations in Groth 16, we represent each bit as 0 or 1 and simulate the following logical operations through arithmetic relations:
Exclusive-or: Use the expression a + b − 2 ab
Negation: Use the expression 1 − a (usually free to incorporate into other constraints)
And: Use the expression a × b
However, operations like rotate-left and other permutation operations are usually considered cost-free operations in the ZK environment and do not require additional constraints.
According to calculations, the number of constraints in each round of Keccak is as follows:
Theta operation generates approximately 4480 constraints
ρ and π operations are zero cost
The χ operation generates approximately 3200 constraints
The operation generates about 64 constraints
Therefore a full Keccak-1600 (24 rounds) would result in 185,856 constraints in Groth 16.
According to the data in Ingonyamas ICICLE library, it takes about 30-40 milliseconds to generate a Keccak ZK proof on an Nvidia 4090 GPU and about 450 milliseconds on a CPU. If 8192 Keccak operations need to be proved, the GPU will take at least 250 to 300 seconds, while the CPU may take nearly an hour.
Attempt 2: Lookup-based Proof Systems
A more modern optimization is to process the data in batches (e.g., 4 or 8 bits) and perform all bit operations using lookup tables. In other words, each 64-bit integer is split into several smaller chunks (e.g., 8 8-bit chunks) and the logical operations are performed using lookup tables.
Specifically, there are the following lookup tables:
XOR lookup table: A 2⁸ × 2⁸ lookup table that computes the XOR of two 8-bit chunks. This allows 8-bit XOR to be done with one constraint instead of the traditional 8 constraints.
AND operation lookup table: It is also a 2 ⁸ × 2 ⁸ lookup table, which is used for the bitwise AND operation of two 8-bit chunks. The effect of saving constraints is similar to XOR.
Rotate-left lookup table: In order to handle the frequently occurring rotate-left operation in Keccak, multiple lookup tables are introduced. Specifically, there are seven lookup tables of size 2⁸, corresponding to rotation distances of 8k+1, 8k+2, etc. (where k is a non-negative integer). Compared to Attempt 1, which does not handle rotation operations at all, this approach introduces additional overhead - about 192 constraints per round. However, this overhead is still relatively small compared to other parts.
In order to implement this system, we no longer use Groth 16, but are more suitable for small domain proof systems such as Stwo and Plonky 3, which have better support for lookup tables. Under this scheme, each complete Keccak operation requires approximately 27,264 constraints, and combined with the call of the lookup table, the overall number of constraints can be greatly reduced, which is significantly optimized compared to Groth 16.
However, this optimization is not absolutely superior in terms of performance. This is because the call and management of the lookup table itself also incurs overhead, which, if not handled properly, may offset the advantage of reducing the number of constraints. Therefore, its actual operating efficiency may not be as good as the implementation based on Groth 16 in some scenarios.
Attempt 3: Binius
Since the speedup brought by lookup tables or customized gates may not be as good as expected in practice, because the overhead of the lookup itself may offset the constraint optimization effect, we need to explore other paths to further improve the efficiency of Keccak proofs.
This is why Keccak is known as the holy grail of zero knowledge. In comparison, earlier hash functions such as SHA-256 and Blake 2/3 also rely on bitwise operations such as XOR and AND, but their biggest performance bottleneck comes from integer addition. Integer addition is usually optimized in proof systems by breaking it into multiple 4-bit blocks, which greatly improves performance. However, Keccak does not involve any integer addition, so these optimization strategies are invalid here.
The most cutting-edge solution at present is Binius. The core idea of this system is that since Keccak is composed entirely of bit operations, we can use a proof system with bits as the basic unit to implement it. This is the breakthrough of Binius.
In Binius, Keccak is represented as an operation over a finite field 𝐹₂ (i.e., a binary field). Since XOR is essentially an addition in 𝐹₂, its associated overhead is almost completely eliminated. The overall process is structured as a series of polynomial operations, and the bit rotation operation can also be easily implemented in the bit-wise processing model. The proof cost is mainly concentrated in the AND gate that appears in the χ step.
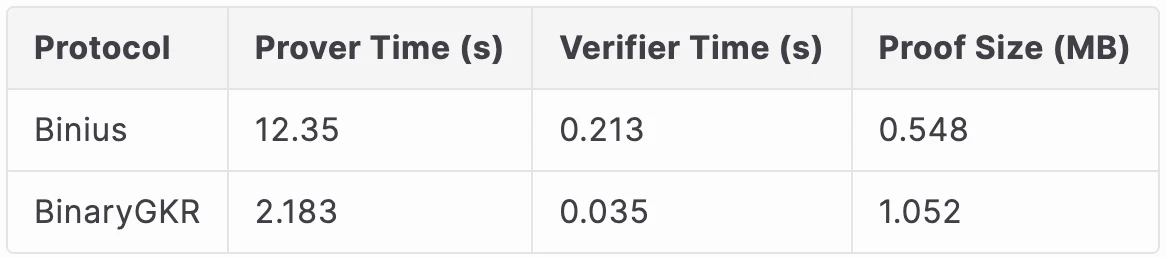
Biniuss benchmark test shows that it only takes about 12.35 seconds to prove 8192 Keccak operations, which is much better than Groth 16 (attempt 1) and the lookup table method (attempt 2).
Is Binius the end? Not really. We found that by removing some redundancy in the Keccak proof, it is possible to further improve the performance by about five times, exceeding the current Binius implementation.
Polyhedra Launches Binary GKR: A Binary Proof System Optimized for Keccak
The Polyhedra team is building a new proof system, Binary GKR (see: ePrint 2025/717 ), which is a framework specifically designed for efficient proof of binary operations, especially for functions like Keccak that are centered on bit operations. The core advantages of Binary GKR come from the following three key technical innovations:
1. Optimize repeated calculations based on the GKR protocol
We choose to base our design of Binary GKR on the GKR protocol (Goldwasser–Kalai–Rothblum) because it can effectively reduce the redundant overhead caused by processing repetitive calculations.
In a typical zkEVM scenario, Keccak often appears as a sidecar prover to batch process a large number of Keccak operations delegated by zkEVM. Therefore, the circuit structure we are targeting naturally has a large number of repetitive patterns, for example: 8192 Keccak calls are a common scale.
More importantly, the Keccak algorithm itself is highly reproducible:
It repeatedly performs similar Boolean operations on a 5 × 5 state matrix;
The whole process consists of 24 rounds of almost identical steps;
The structures of each round are the same, only the input states are different.
Such characteristics make Keccak a natural adapter for the GKR protocol:
Verifier has low cost and is suitable for high-frequency verification scenarios;
Prover can make full use of structural repetitiveness, reuse computational paths, and greatly simplify proof overhead;
Compared with traditional general proof systems, it has significant performance advantages in batch Keccak scenarios.
2. Polynomial Commitment Based on Binary Field
We use a polynomial commitment scheme based on linear codes that operates directly on the binary field. As we mentioned earlier, using a native binary representation allows us to get operations such as XOR for free. In addition, similar to Biniuss method, polynomial commitment based on the binary field avoids the redundancy caused by using a larger number field, which significantly improves the system in terms of performance and efficiency.
3. Precomputed tables for binary operations
The key innovation in the Binary GKR paper is that it significantly improves the proof efficiency of the GKR protocol by fully utilizing the high sparsity of the circuit structure. This sparsity is preserved even when processing multiple bits at the same time. What we do is pack multiple bits into polynomials in the GKR protocol (note: these are intermediate polynomials and do not require commitment), and then perform the GKR protocol operations directly on these packed data.
Since the sparsity is still high, we can use precomputed tables to allow the prover to generate proofs with much lower computational overhead than the traditional GKR protocol. This optimization significantly improves the efficiency of GKR when processing binary relations.
This article will focus on the third technical optimization mentioned above: precomputed tables for binary operations.
Packing bits into polynomials
The core of our solution is a new GKR protocol sumcheck method designed for data-parallel Boolean circuits. This method packs multiple bits into a polynomial, effectively reducing the provers computational burden and significantly improving efficiency.

Evaluating binary relations more efficiently
Compared with traditional GKR, Binary GKR brings new optimization space.


The preprocessing table is very small. By setting parameters appropriately, we can keep the table size to about 15 MB. This size can easily fit into the CPUs L3 cache, making the table lookup operation very efficient.
This technique is applicable to almost all binary operations and is the core of the performance improvement in the Binary GKR construction.
Implementation and Evaluation
We implemented the SNARK system in Rust based on the arkworks ecosystem and conducted comprehensive benchmarks on random Boolean circuits of different sizes.
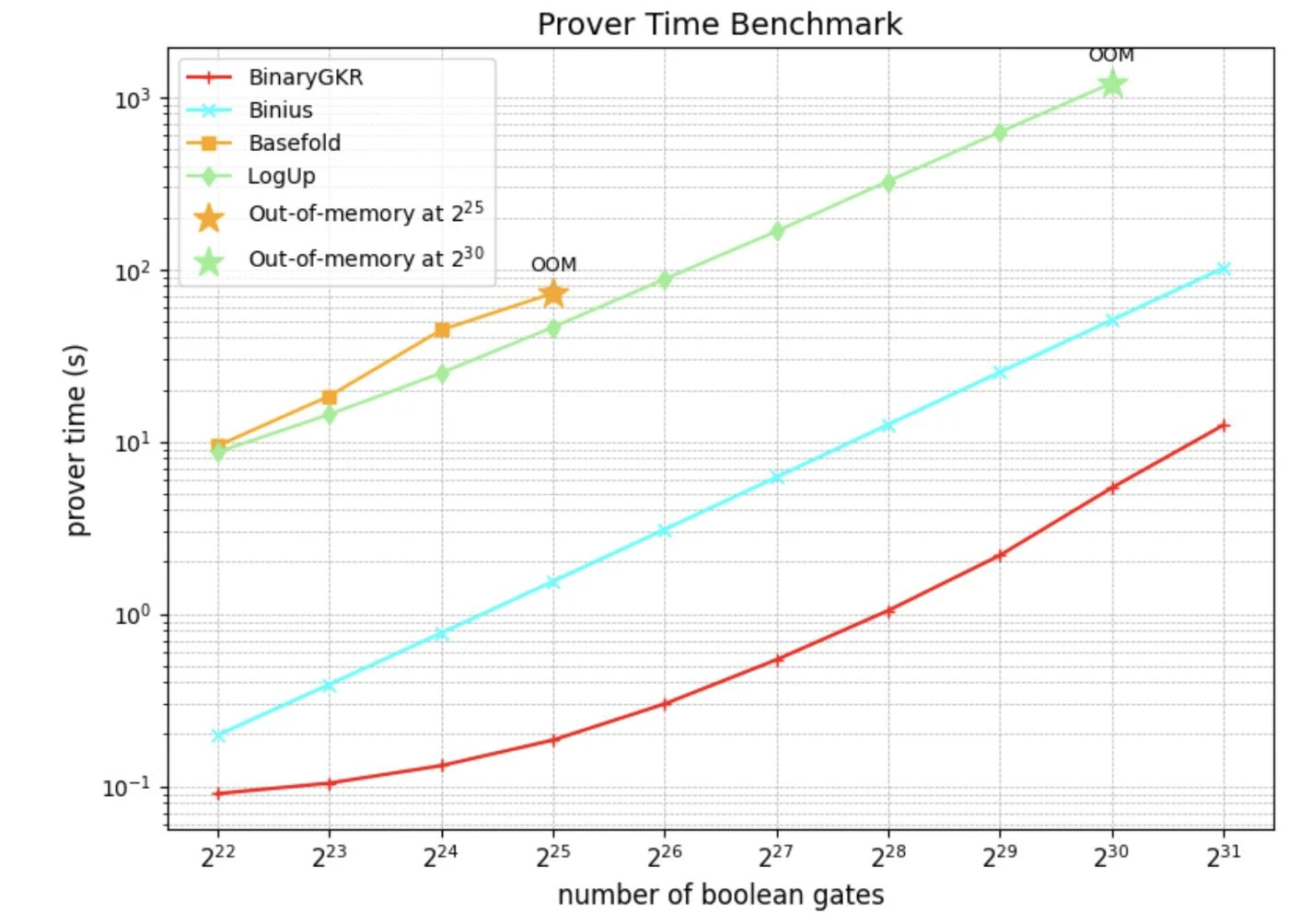
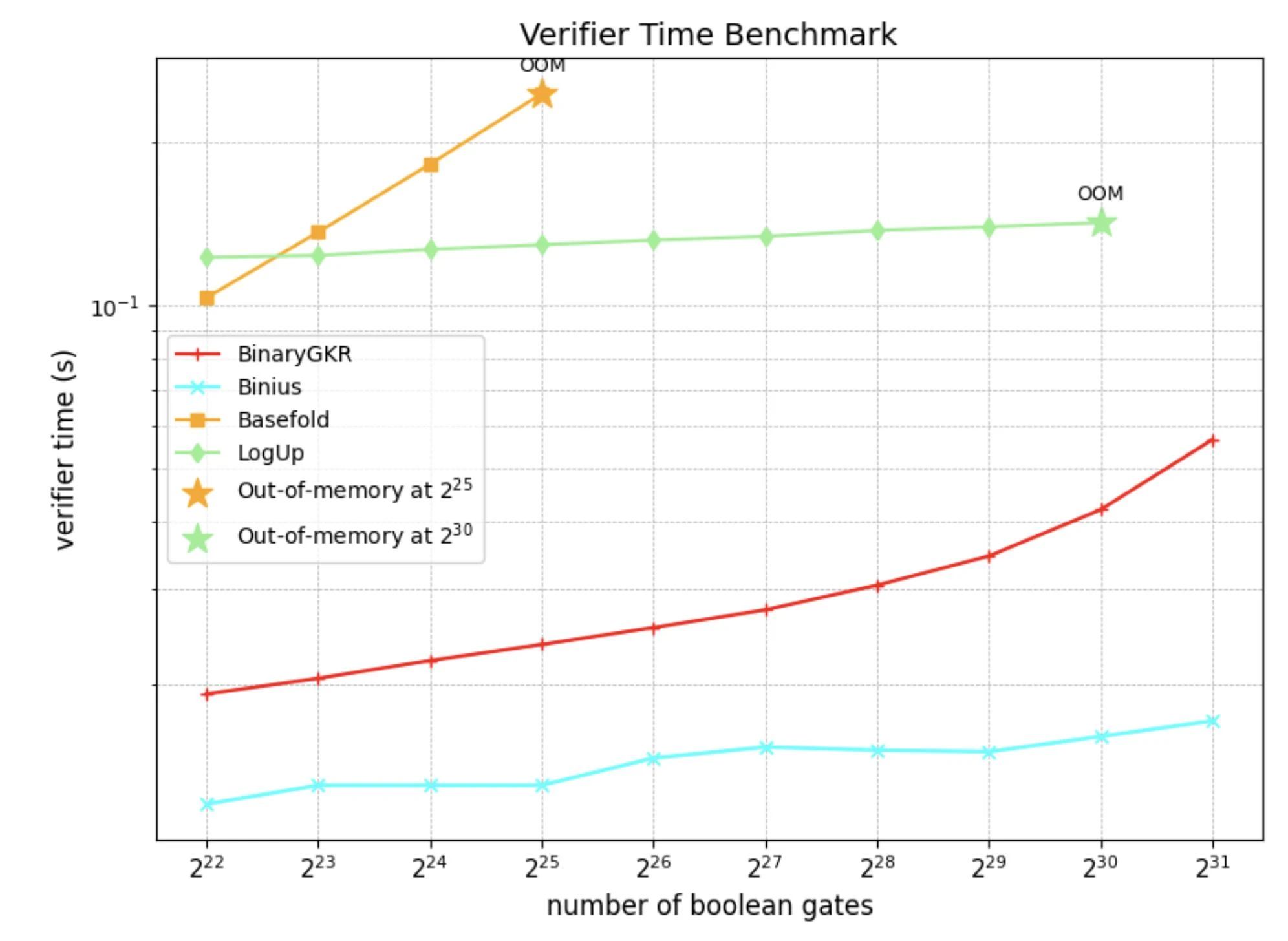
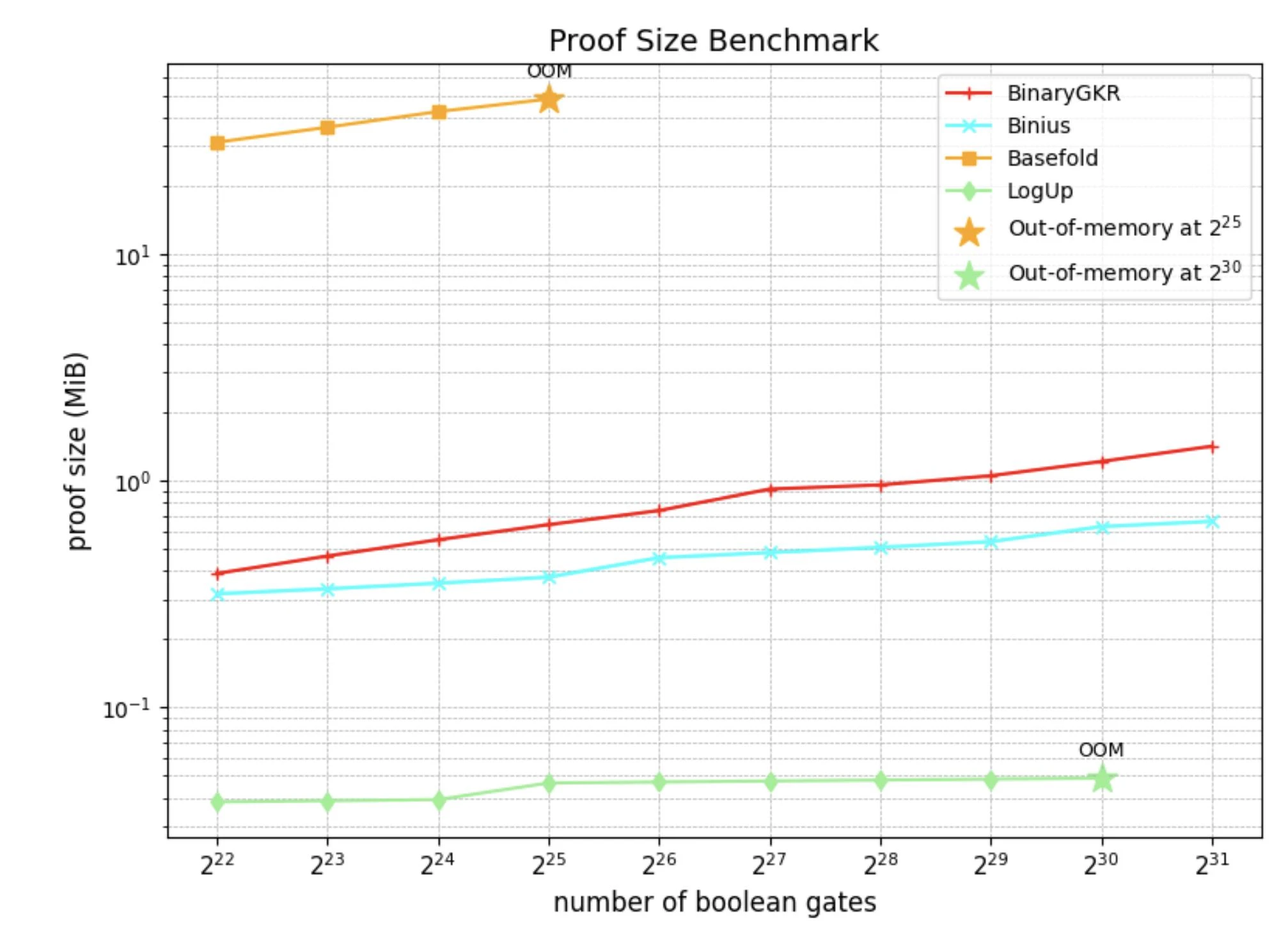
In addition to random Boolean circuits, we also focus on the holy grail of zero-knowledge proofs - Keccak. We compare the performance of the proposed method with Binius on Keccak proofs. Both are based on binary field operations.
When processing 8192 Keccak calls, Binius takes 12.35 seconds to generate a proof, while our method only takes 2.18 seconds. At the same time, thanks to the concise structure of Keccak, our verification time is also shorter, only 0.035 seconds. In terms of communication overhead, the size of our proof is 1.052 MB.
Conclusion
This article introduces the latest progress of the Polyhedra team in the field of zero-knowledge proof, focusing on the optimization of binary functions such as Keccak. This achievement can be used as an efficient auxiliary module for various zkEVM constructions.
We plan to integrate Binary GKR into zkEVM systems such as RISC Zero and SP 1 to further verify its role in alleviating Keccak performance bottlenecks. The ultimate goal is to accelerate Ethereums progress towards full SNARKization of layer-1 without destroying the existing EVM architecture.
Original link: https://blog.polyhedra.network/binary-gkr/










